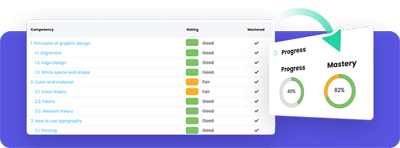
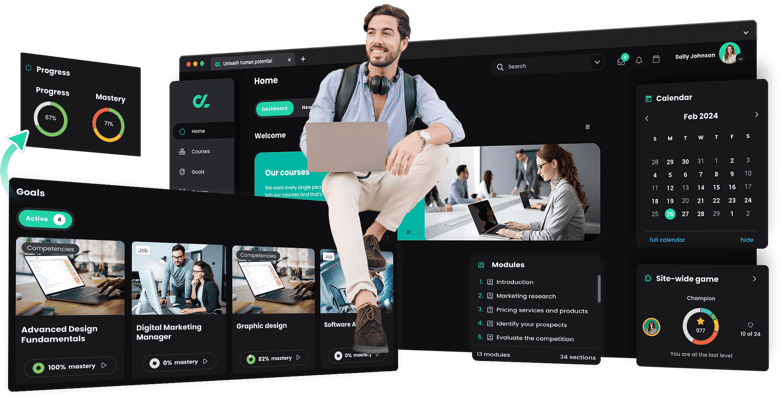
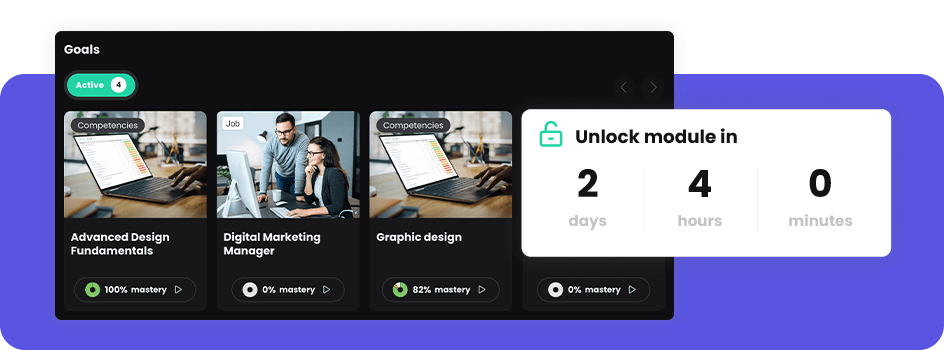
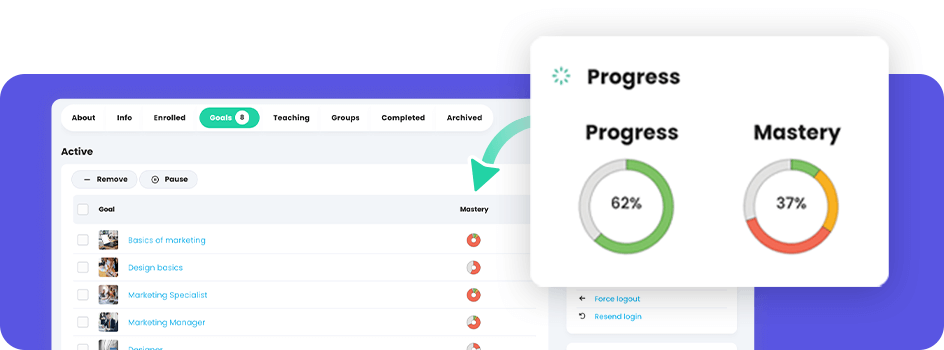
CYPHER is a finalist for three EdTech Awards 2024
Read moreTHE GENERATIVE LEARNING PLATFORMMove faster with an AI-powered learning platform
CYPHER's learning platform helps you to be ready for whatever comes your way. Combining the powers of LMS, LXP, and course development tools you'll:
- Create courses faster
- Train and teach better
- Learn even quicker






Your way. Not theirs.
Traditional learning management software is bloated requiring big budgets. Their complex processes and software overkill leave you stuck trying to figure out how to use the LMS their way instead of your way. Get more things done with the most innovative AI-powered learning platform from CYPHER. Get it your way no matter the size of your business or academic institution.
Their way
Your way
Cost to create and deliver a course
Cost to create and deliver a course
Research and create content, images, assessments, competencies
Automate course creation from content to competencies to quizzes
Time to create a course
Time to create a course
Courses become out of date and require manual updating
Courses stay up-to-date as business needs change
Best practices from CYPHER customers
CNN amazed by AI 360 course creation
Choose your powers!
Your path. Your pace. Your potential.
Start your journey with our Learning Management System (LMS) for solid foundations, then amplify your capabilities when the time is right. Elevate your learning initiatives with our Learning Experience Platform (LXP) capabilities for personalized and engaging content delivery. And when you're ready to create your own content, unlock the full potential of leading AI innovation with our robust content development tools.
It's your path, your pace, your powers – tailor your learning journey your way.

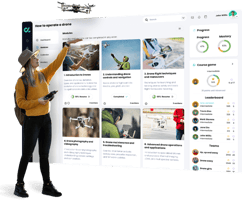
LEARNING MANAGEMENT POWERS
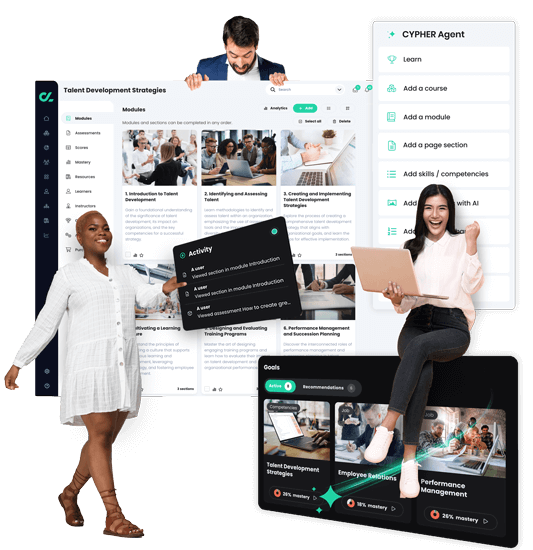
Give learners what they need, before they need it
Our award-winning learning management software that helps you move faster on learning initiatives than ever before.

LEARNING EXPERIENCE POWERS
Deliver highly personalized learning in less time
LXPs are more than just a new LMS—it’s a whole new way for all to learn and grow while saving time and resources.

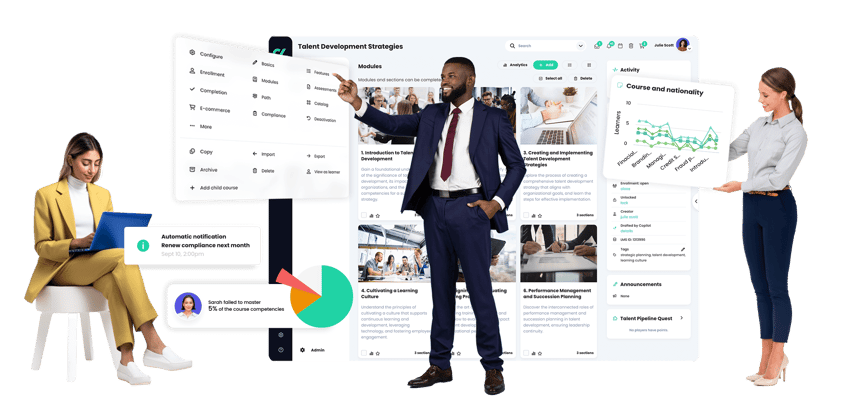
COURSE DEVELOPMENT POWERS
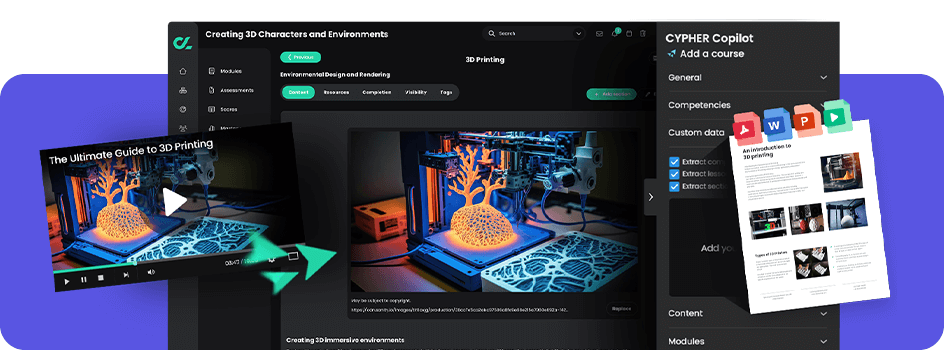
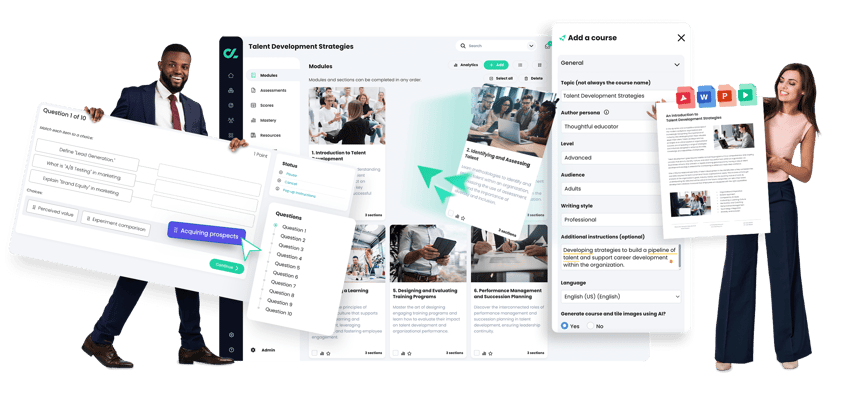
Build courses faster—no experience required
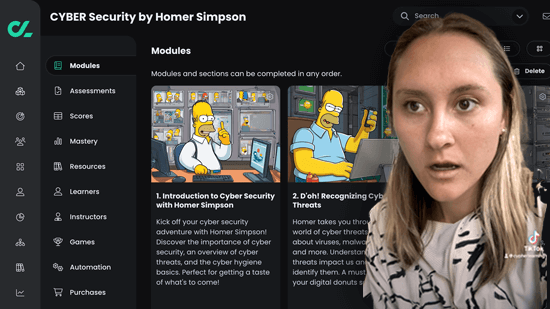
AI 360 with Copilot accelerates the creation of competency-based, gamified courses, with assessments in minutes.
LEARNING MANAGEMENT POWERSThe LMS for leaders looking for a big advantage
LEARNING EXPERIENCE POWERSCreate bigger impact. Deliver the right course at the right time in the right way.
COURSE DEVELOPMENT POWERSThe fastest way to create a course with competencies, assessments, & more - in minutes
AI 360 accelerates course creation in minutes - all mapped to competencies, assessments and more. More
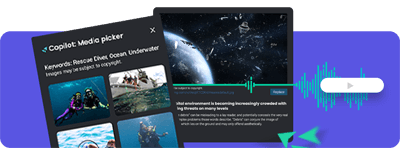
Turning static courses into multisensory learning experiences. Save time and resources. More
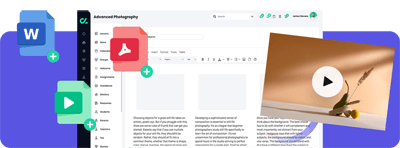
Upload proprietary resources like video or PDFs to create training specific to your terminology and brand. More

Handle repetitive tasks effortlessly. Platform-wide automation that accelerates productivity. More
1 platform. 3 powers. Limitless solutions.
From customer training to partner training to onboarding to mentorship to certification to compliance. We make it a reality.
- Extended enterprise
- Employee and growth
- Product and enablement
- Academia
Powering millions of learning journeys
"The innovation that has been driven out of this platform in the last 12 months is just really jaw dropping and astounding."
John Leh
CEO, Talented Learning
"Moving through the platform is intuitive and fast. The best way to describe the tech is to say it anticipates the moves of the learner. And it’s super powerful."
Michael Rochelle
Brandon Hall Group
Award-winning platform

















"Artificial Intelligence Solution," "Content Provider Solution," and "LMS Solution."
Looking for clear-cut answers to your AI questions? Graham Glass, CEO and Founder, CYPHER Learning can help.

Forbes Advisor ranks CYPHER as Best LMS, Enterprise LMS, and Employee Training Software - 2 years in a row!

Non-compliant workers cost organizations on average $1.6m yearly, discover the importance of education.
AI tool boosts trainee pass rates in medical coder certification tests
Generative learning platform CYPHER Learning has raised pass rates on certification exams for students at the The Health Information Management Training Institute (HIMTI), HIMTI said. HIMTI students... Press coverage May 1, 2024Exploring The Future Of Generative AI In Learning
Graham Glass converses with Brandon Hall Group's Chief Strategy Officer Michael Rochelle about GenAI's potential to transform the learning and development landscape. Listen to the full podcast. Press coverage May 1, 2024Are You An Introvert? 19 Tips To Elevate Your People Management Skills
Graham Glass provides his take on how organizations can uplevel their people management skills in this latest Forbes article. Press coverage May 1, 2024Revolutionizing Compliance Training
Brandon Hall Group dived into our latest compliance research to discuss how AI can help organizations create better compliance training courses that help them avoid costly compliance mistakes. Read... Press coverageAs seen in